递归算法破解迷宫、汉诺塔与八皇后:深入Java实现策略
递归算法作为一种强大的编程技巧,在解决复杂问题时显得尤为有效。本文将探讨递归算法在破解迷宫、汉诺塔与八皇后问题中的应用,并深入解析其在Java中的实现策略。
递归算法破解迷宫、汉诺塔与八皇后:深入Java实现策略,主要涉及递归算法在这三个经典问题中的具体应用。迷宫问题要求找到一条从入口到出口的路径;汉诺塔问题则需要将三个大小不同的盘子从一个柱子移动到另一个柱子,且每次只能移动一个盘子;八皇后问题则是要在8x8的棋盘上放置8个皇后,使得她们之间互不攻击。
迷宫问题的递归解决策略是通过不断地探索相邻的单元格,当遇到死路时回溯至上一个单元格,继续探索其他可能的路径。在Java中,可以使用二维数组表示迷宫,递归函数接收当前位置和迷宫数组作为参数,当找到出口时返回成功。
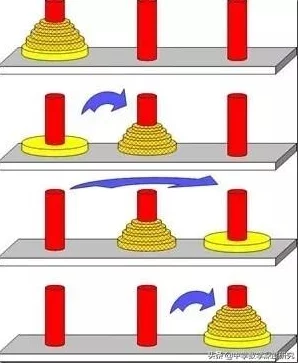
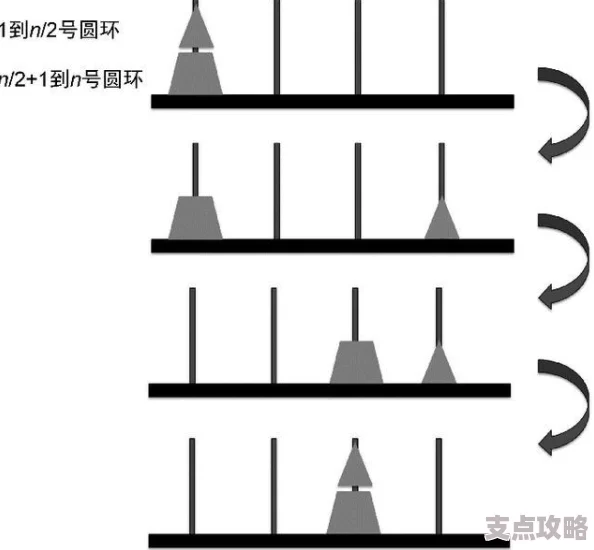
汉诺塔问题的递归解决策略是将问题分解为三个子问题:将n-1个盘子从源柱子移动到辅助柱子,将最大的盘子从源柱子移动到目标柱子,再将n-1个盘子从辅助柱子移动到目标柱子。在Java中,可以定义一个递归函数,接收盘子数量、源柱子、辅助柱子和目标柱子作为参数。
八皇后问题的递归解决策略是逐行放置皇后,并检查当前位置是否与已放置的皇后冲突。在Java中,可以使用一维数组表示棋盘,递归函数接收当前行和棋盘数组作为参数,当放置完所有皇后时返回成功。
以下是针对这三个问题的具体探讨:
1. 迷宫问题:递归算法在迷宫问题中的应用表现为,当遇到死路时,递归地回溯至上一个单元格,尝试其他可能的路径。在Java中,可以使用以下代码表示递归函数:
```java
public boolean solveMaze(int[][] maze, int x, int y) {
if (x = maze.length || y = maze[0].length || maze[x][y] == 1) {
return false;
}
if (x == maze.length - 1 && y == maze[0].length - 1) {
return true;
}
maze[x][y] = 1; // 标记为已访问
return solveMaze(maze, x + 1, y) || solveMaze(maze, x, y + 1);
}
```
2. 汉诺塔问题:递归算法在汉诺塔问题中的应用表现为,将问题分解为三个子问题,递归地解决这三个子问题。在Java中,可以使用以下代码表示递归函数:
```java
public void hanoi(int n, char from, char to, char aux) {
if (n == 1) {
System.out.println("Move disk 1 from " + from + " to " + to);
return;
}
hanoi(n - 1, from, aux, to);
System.out.println("Move disk " + n + " from " + from + " to " + to);
hanoi(n - 1, aux, to, from);
}
```
3. 八皇后问题:递归算法在八皇后问题中的应用表现为,逐行放置皇后,并检查当前位置是否与已放置的皇后冲突。在Java中,可以使用以下代码表示递归函数:
```java
public boolean isSafe(int[] board, int row, int col) {
for (int i = 0; i < row; i++) {
if (board[i] == col || Math.abs(i - row) == Math.abs(board[i] - col)) {
return false;
}
}
return true;
}
public boolean solveNQueens(int[] board, int row) {
if (row == board.length) {
return true;
}
for (int i = 0; i < board.length; i++) {
if (isSafe(board, row, i)) {
board[row] = i;
if (solveNQueens(board, row + 1)) {
return true;
}
}
}
return false;
}
```
相关问题及解答:
1. 递归算法在解决迷宫问题时,如何避免重复探索已访问的单元格?
答:在递归函数中,可以通过标记已访问的单元格(如将单元格值设置为1)来避免重复探索。
2. 汉诺塔问题中,递归算法的复杂度是多少?
答:汉诺塔问题的递归算法复杂度为O(2^n),其中n为盘子的数量。
3. 八皇后问题中,递归算法的时间复杂度是多少?
答:八皇后问题的递归算法时间复杂度为O(N!),其中N为皇后的数量。