C语言实现最大公约数的多种方法-探索高效算法技巧
### C语言实现最大公约数的多种方法-探索高效算法技巧
最大公约数(Greatest Common Divisor, GCD)的计算在计算机科学以及数学领域中具有广泛的应用,例如分数化简、数据处理以及加密算法等。如何利用C语言高效地实现最大公约数的计算,既涉及算法设计,又直接影响程序运行效率。本文将从多种算法的原理与实现角度,探讨最大公约数的求解方法及优化策略。
#### 1. 辗转相除法:经典而高效的解决方案
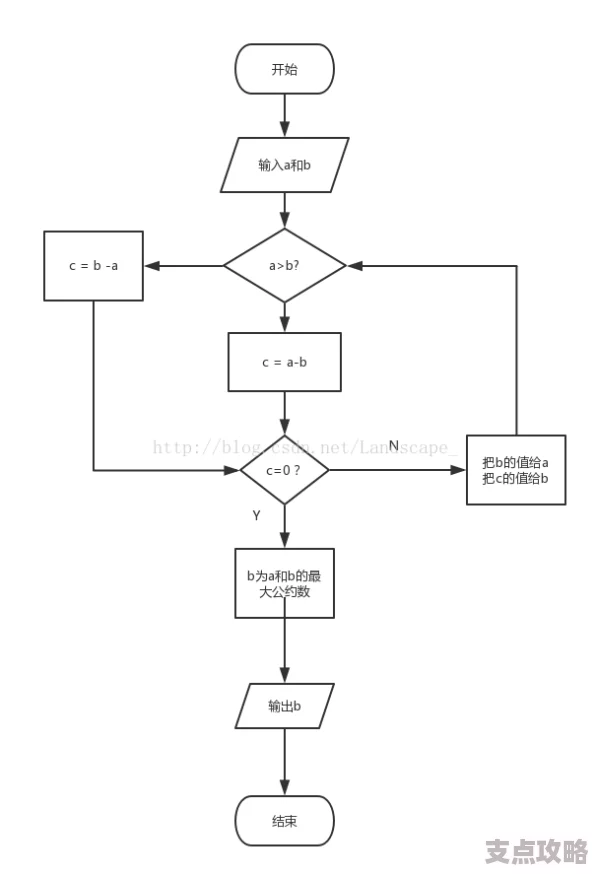
辗转相除法(即欧几里得算法)是一种快速计算最大公约数的经典方法,基于这样一个定理:两个整数的最大公约数等于较大数与较小数的余数的最大公约数。例如,对于两个正整数 a 和 b(假设 a > b),可以用以下公式重复计算:
```
GCD(a, b) = GCD(b, a % b)
```
直到 b 等于零,此时 a 即为两数的最大公约数。这种方法的实现代码如下:
```c
#include
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
int main() {
int a = 56, b = 98;
printf("GCD of %d and %d is %d\n", a, b, gcd(a, b));
return 0;
}
```
该算法的时间复杂度为 O(log(min(a, b))),具有很高的效率。这主要得益于对数的性质:每次模运算后,a 和 b 的数值都会快速减小。
#### 2. 扩展欧几里得算法:计算线性表示
扩展欧几里得算法不仅可以计算最大公约数,还能找到整数 x 和 y,使得 ax + by = gcd(a, b)。这一功能在许多密码学场景和整数运算问题中有重要应用。
扩展欧几里得算法的实现稍微复杂一些,以下是示例代码:
```c
#include
int extendedGCD(int a, int b, int* x, int* y) {
if (b == 0) {
*x = 1;
*y = 0;
return a;
}
int x1, y1;
int gcd = extendedGCD(b, a % b, &x1, &y1);
*x = y1;
*y = x1 - (a / b) * y1;
return gcd;
}
int main() {
int a = 56, b = 98, x, y;
int gcd = extendedGCD(a, b, &x, &y);
printf("GCD of %d and %d is %d\n", a, b, gcd);

printf("Coefficients x = %d, y = %d\n", x, y);
return 0;
}
```
扩展欧几里得算法的复杂度与普通欧几里得算法相同,即 O(log(min(a, b))),但适用范围更广。
#### 3. 穷举法:简单但低效
穷举法是一种最直观的最大公约数求解方法:从较小数开始向下遍历,找到能同时整除两个数的最大整数。虽然原理简单,但效率较低,特别是对于大数计算时。
实现如下:
```c
#include
int gcdExhaustive(int a, int b) {
int gcd = 1;
for (int i = 1; i b ? b : a); i++) {
if (a % i == 0 && b % i == 0) {
gcd = i;
}
}
return gcd;
}
int main() {
int a = 56, b = 98;
printf("GCD of %d and %d is %d\n", a, b, gcdExhaustive(a, b));
return 0;
}
```
穷举法的时间复杂度为 O(min(a, b)),效率远低于欧几里得算法,因此仅适用于小规模数据或教学演示场景。
#### 4. 连续减法法:适合低硬件性能条件的算法
连续减法法的思路来源于欧几里得算法,但无需使用取模运算,而是通过减法逐步缩小 a 和 b 的值,直至两者相等。此时的数值即为最大公约数。
代码实现如下:
```c
#include
int gcdSubtract(int a, int b) {
while (a != b) {
if (a > b)
a -= b;
else
b -= a;
}
return a;
}
int main() {
int a = 56, b = 98;
printf("GCD of %d and %d is %d\n", a, b, gcdSubtract(a, b));
return 0;
}
```
减法法的效率较低,尤其是 a 和 b 差值较小时,运算次数会增加,时间复杂度近似为 O(max(a, b))。
#### 5. 二进制法(Stein算法):数学与计算结合的优化方案
二进制法利用了二进制表示和移位运算的特性,通过优化计算减少复杂度。基本原理如下:
- 如果 a 和 b 均为偶数,则 GCD(a, b) = 2 * GCD(a/2, b/2);
- 如果 a 是偶数而 b 为奇数,则 GCD(a, b) = GCD(a/2, b);
- 如果 a 和 b 均为奇数,则 GCD(a, b) = GCD((a-b)/2, b) (确保 a ≥ b);
- 重复上述过程,直至 a、b 中一个数为零,另一个数即为最大公约数。
以下是用 C 实现的代码:
```c
#include
int gcdBinary(int a, int b) {
if (a == 0) return b;
if (b == 0) return a;
int shift;
for (shift = 0; ((a | b) & 1) == 0; shift++) {
a >>= 1;
b >>= 1;
}
while ((a & 1) == 0)
a >>= 1;
do {
while ((b & 1) == 0)
b >>= 1;
if (a > b) {
int temp = a;
a = b;
b = temp;
}
b = b - a;
} while (b != 0);
return a << shift;
}
int main() {
int a = 56, b = 98;
printf("GCD of %d and %d is %d\n", a, b, gcdBinary(a, b));
return 0;
}
```
二进制法避免了复杂的除法运算,适合低性能处理器或嵌入式设备,时间复杂度与欧几里得算法相近。
---
#### 提问与解答
**1. 为什么二进制法在某些场景下更适合使用?**
答:二进制法利用移位运算代替取模和除法运算,这对于不具备高效除法指令的处理器(如嵌入式系统或某些硬件)尤为高效。此外,它结合了数据的二进制表示方式,与现代计算机存储和运算特性更契合。
**2. 扩展欧几里得算法的实际应用有哪些?**
答:扩展欧几里得算法在数论领域非常重要,例如计算模逆元、解决线性不定方程,以及在公钥加密算法(如 RSA)中用于生成密钥。
**3. 如何选择最适合的最大公约数算法?**
答:选择算法取决于应用场景。如果追求效率并应用于大数计算,优先选择辗转相除法或二进制法;对于需要额外结果(如线性表示)的场景,使用扩展欧几里得算法;穷举法和连续减法法更多使用于教学演示和简单场景中。